Institut za
oceanografiju i ribarstvo
More ima ključnu ulogu regulatora klime i ublažavanja štetnih učinaka klimatskih promjena.
20.04.24 07:50
11.2
°C
TEMPERATURA ZRAKA
57
%
VLAŽNOST ZRAKA
199
W/m2
SUNČEVO ZRAČENJE
53
° (SI)
SMJER VJETRA
6
MED
UV ZRAČENJE
1.8
m/s
BRZINA VJETRA
1009.4
hPa
TLAK ZRAKA
Novosti
Prva nacionalna znanstveno-istraživačka institucija koja se bavi istraživanjem mora.
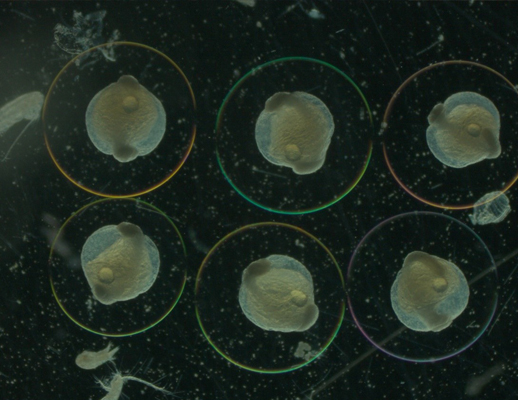
Institut provodi znanstvena istraživanja iz područja biološke, kemijske i fizičke oceanografije, sedimentologije, te ribarstvene biologije i marikulture.










Sudjelujte u istraživanju
Želite biti aktivni članovi zajednice i surađivati s nama? Podijelite svoja otkrića i fotografije zanimljivih morskih organizama i pojava.
Projekti
Institut provodi veliki broj nacionalnih i međunarodnih projekata.